El polinomio de Taylor, es una herramienta usada en el campo de aproximación de funciones, que nos permite expresar cualquier tipo de función, de una forma polinómica particularmente aproximada. Su uso, al menos en un sentido, es para evaluar funciones de forma aproximada. Sin más dilación, comenzemos a introducir el tema:
Considerando una función $f$, siendo aproximada en torno a un punto $a \in Dom(f)$: El polinomio de Taylor de grado "$n$" denotado por $P_{n,a}$ se expresará como:
$\mathbf{P_{n,a}=f(a)+\frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3... \frac{f^{n)}(a)}{n!}(x-a)^n}$
O más brevemente como: $P_{n,a}=\sum _{i=0}^{n} \frac{f^{i)}(a)}{i!}(x-a)^i$
NOTA: En el anterior apunte, se entiende que trabajamos con una función de indefinida cantidad de derivadas. Por lo que la aproximación de Taylor, en casos distintos, simplemente acabaría en el grado en el que tenemos una constante en el numerador.
Ya que tenemos definido el polinomio de Taylor, empezemos a experimentar con la función más clásica de los profesores: $f(x)=\sin x$. Como debemos escoger un punto entorno al cual hacer la aproximación, vamos a probar con $x=0$.
Empezemos a calcular el polinomio de Taylor de grado 0:
$P_{0,0}=\sin 0=0$
Para el polinomio de grado uno, tenemos:
$P_{1,0}=\sin 0 \ + \frac{\sin ' (0)}{1!} (x-0)=x$
Para el de grado dos:
$P_{2,0}=x + \frac{\sin '' (0)}{2!}x^2\Rightarrow x$
$P_{3,0}=x + \frac{\sin ''' (0)}{3!}x^3 = x-\frac{1}{6}x^3=\frac{6x-x^3}{6}$...
Si graficamos cada polinomio de Taylor y lo comparamos con la gráfica de la función seno...
..., vemos que mientras mayor grado presente el polinomio de Taylor, mejor será la aproximación en torno a $x=0$. Esto se claramente si tratamos de obtener el valor del seno de π por ejemplo:
Por lo que, usando esta herramienta podemos escribir la función seno de forma polinómica:
$$\sin x = \frac{1}{1!}x + \frac{-1}{3!}x^3+\frac{1}{5!}x^5=\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}x^{2n+1}$$
Volviendo al tema, para acotar el error de las aproximaciones de un polinomio de Taylor, se recurre al resto de Lagrange:
Teniendo un polinomio de Taylor, de grado $n$ y aproximado en torno a $x_0=a$; el resto de Lagrange se define por:
$\mathbf{R_n (x)=\frac{f^{n+1)}(\theta)}{(n+1)!} (x-a)^{n+1} \ \ \ ,\theta \in (a,x)}$
Nota: el coeficiente $x$ de la fórmula, es el punto en el que se investiga el valor aproximado de la función original. Por ejemplo, si investigamos $cos (\pi /2)$ a través del polinomio de Taylor, $x=\pi /2$.
De esta manera, el error resultará ser el valor absoluto del resto de Lagrange; que será acotado con el rango de valores posibles para θ:
$\mathbf{E=|R_n (x)|\ \ \ ,\theta \in (a,x)}$
Resolvamos ejercicios de varios tipos para profundizar en el tema:
Aproxima el valor de $\mathbf{e^{1.45}}$ usando el polinomio de Taylor de grado $\mathbf{n=2}$ en torno a $\mathbf{x_0 = 1}$. Posteriormente, acota el error en la aproximación.
Obtener $\sqrt[5]{1.5}$ con una aproximación inferior a una diezmilésima utilizando el polinomio de Maclaurin de la función $f(x)=\sqrt[5]{1+x}$.
En posteriores posts, aplicaremos esta poderosa herramienta para el cálculo de límites e integrales especiales. Gracias por leer.
BIBLIOGRAFÍA:



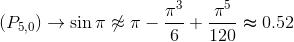






Comentarios
Publicar un comentario